Unit 5: How Radical Are You?

• This unit focuses on simplifying radical expressions and performing operations involving radicals.

Reading Process

Vocabulary Development

• The student will use new vocabulary that is introduced and taught directly.
• The student will listen to, read, and discuss familiar and conceptually challenging text.
• The student will relate new vocabulary to familiar words.

Algebra Body of Knowledge

• Radical Expressions and Equations
• Simplify radical expressions.
• Add, subtract, multiply, and divide radical expressions (square roots and higher).

Lesson 1: Simplifying Radical Expressions

We will see that radical expressions can be rewritten to conform to the mathematical definitions of simplest terms. We will then be able to perform the operations of addition, subtraction, multiplication, and division on these reformatted expressions. We will also explore the effects of multiplying a radical expression by its conjugate.

Reading Process

Vocabulary Development

• The student will use new vocabulary that is introduced and taught directly.
• The student will listen to, read, and discuss familiar and conceptually challenging text.
• The student will relate new vocabulary to familiar words.

Algebra Body of Knowledge

Radical Expressions and Equations

• Simplify radical expressions.

Radical Expressions and Equations

Adding and subtracting radical expressions involves combining terms with square roots or other radical symbols. To add or subtract radical expressions, follow these steps:

1. Identify Like Terms: Look for radical expressions with the same radical symbol and the same radicand (the expression inside the radical).

2. Perform the Operation: Add or subtract the coefficients of the like terms while keeping the radical symbol and the radicand unchanged.

3. Combine Like Terms: After performing the operation, if possible, combine any like terms outside the radical symbol.

4. Simplify: If necessary, simplify the resulting expression by simplifying any radicals.

5. Check for Extraneous Solutions: Sometimes when simplifying radicals, you might introduce extraneous solutions that are not valid. Always check your final solution to ensure it satisfies any given restrictions or conditions.

• Add, subtract, multiply, and divide radical expressions (square roots and higher).

Radical expressions are called radical expressions if the indexes are identical, and the radicands are the same. They $4\sqrt[3]{5x}$are like radical expressions since the indexes are the same and the radicands are similar, but $\sqrt[3]{5x}$they are not like radical expressions since their radicands are not identical. Radical expressions can be added or subtracted only if they are like radical expressions.

Lesson 3: Multiply and Divide Radical Expressions

Radical Expressions and Equations

• Add, subtract, multiply, and divide radical expressions (square roots and higher).

Multiplying and dividing radicals uses the 'Product Rule' and the 'Quotient Rule' as seen at the right. The 'n' means that the index could be any value.

Product Rule

$\sqrt[n]{ab}=\sqrt[n]{a}\times \sqrt[n]{b}$

where a ≥ 0, b≥ 0

'The radical of a product is equal to the product of the radicals of each factor.'

Quotient Rule

$\sqrt[a]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}$

where a ≥ 0, b > 0

'The radical of a quotient is equal to the quotient of the radicals of the numerator and denominator.'

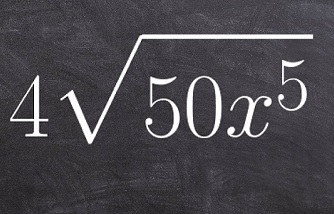
Lesson 4: Multiple Terms and Conjugates

Vocabulary Development

• The student will use new vocabulary that is introduced and taught directly.

Algebra Body of Knowledge

Radical Expressions and Equations

• Add, subtract, multiply, and divide radical expressions (square roots and higher).