Unit 2 Lesson 5 Reasoning in Algebra and Geometry

Unit 2 Lesson 5: Reasoning in Algebra and Geometry

Unit 2 Lesson 5 Reasoning in Algebra and Geometry Banner

Lesson Overview

Reasoning in Geometry

What You Will Learn

applying logical reasoning in algebraic and geometry situations
how to use valid statements and justifications when writing proofs

Additional Resources

Overview

I Geometry Shape n this lesson, you will learn to apply logical reasoning to algebraic and geometric situations. You will show your understanding by using valid statements and justifications to write proofs.

Essential Understanding

Algebraic properties of equality are used in geometry. They will help you solve problems and justify each step you take. In geometry, you accept postulates and properties as true. Some of the properties that you accept as true are the properties of equality from algebra. You use deductive reasoning when you solve an equation. You justify each step with a postulate, property, or a definition.

Lesson 5: Reasoning in Algebra and Geometry

Additional Resources (Reasoning in Algebra and Geometry)

Proceed to Next Page

Prepare for Application

Instructions

You have now studied Reasoning in Algebra and Geometry. It is now time to demonstrate your learning.

Try the activities below on your own. You should be able to answer these before beginning the practice.

Do these activities in your journal.

Activity 1

What is the value of x? Justify each step.

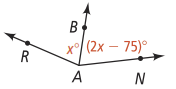
Activity 1

Given: $\vec{A B}$ bisects $∠ R A N$

Activity 2

What is the name of the property of equality or congruence that justifies from going from the first statement to the second statement?
1. $\bar{A R} ≅ \bar{T Y}$ , $\bar{T Y} ≅ \bar{A R}$
2. 3( x + 5) = 9 , 3x + 15 = 9
3. $\frac{1}{4} x = 7$ , x = 28
What property justifies the statement $m ∠ R = m ∠ R$ ?

Activity 3

Write a two-column proof.
Given: $\bar{A B} ≅ \bar{C D}$
Prove: $\bar{A C} ≅ \bar{B D}$
In problem 3 on page 116 of your textbook, why is Statement 2 necessary in the proof?