Unit 3 Lesson 7 Equations of Lines in the Coordinate Plane
Unit 3 Lesson 7: Equations of Lines in the Coordinate Plane
Lesson Overview
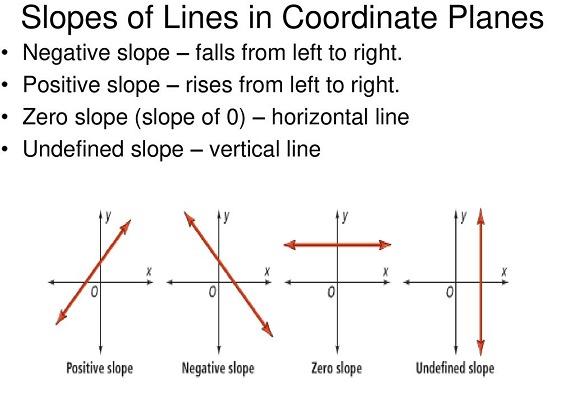
What is Slope?
What You Will Learn
- The concept of slope and how it relates to the graph and the equation of a line
Overview
The steepest hill has the most significant slope. In this lesson, you will explore the concept of slope and how it relates to the graph and the equation of a line.
Essential Understanding
You can graph a line and write its equation when you know specific facts, such as its slope and a point on the line.
This course is based on a textbook that is viewable by clicking on the textbook icon. Keep the textbook open while you go through the lesson so that you may refer to it throughout the lesson.
Additional Resources
Lesson 7: Equations of Lines in the Coordinate Plane
Additional Resources (Equations of Lines in the Coordinate Plane)
Proceed to the Next Page
Prepare for Application
Instructions
You have now studied Exploring Angle Pairs. It is now time to demonstrate your learning.
Try the activities below on your own. You should be able to answer these before beginning the practice.
Do these activities in your journal.
Activity 1
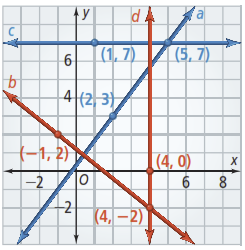
Use the graph below for questions 1-2.
- What is the slope of line a?
- What is the slope of line c?
Activity 2
Refer to Problem 4 on page 192 of your textbook for questions 1-2.
1. What is the equation of the line in Problem 4 if you use (-2, -1) instead of (3, 5) in the last step?
2. Rewrite and compare the equations in Problem 4 and Question 1 in slope-intercept form. What can you conclude?
Activity 3
Graph
- y = 3x - 4.
- .
Activity 4
1. What is an equation of the line with slope and y-intercept 2?
2. What is an equation of the line through (-1, 4) with slope -3?
Activity 5
- What are the equations of the horizontal and vertical lines through (4, -3)?
- Can you write the equation of a vertical line in slope-intercept form? Explain.