Unit 4 Lesson 2 Triangle Congruence by SSS and SAS
Unit 4 Lesson 2: Triangle Congruence by SSS and SAS
Lesson Overview
SSS & SAS
What You Will Learn
- how to prove congruence with a standard recurring scenario among two triangles
- SSS
- SAS
Overview
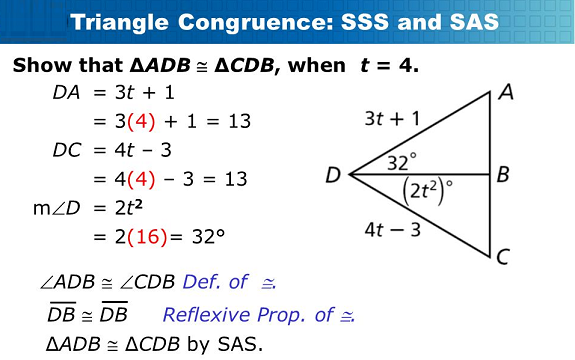
In Lesson 4-1, you learned that the triangles are congruent if two triangles have three congruent corresponding angles and three congruent corresponding sides. In this lesson, you will prove that two triangles are congruent with less information.
Essential Understanding
You can prove that two triangles are congruent without showing that all corresponding parts are congruent. In this lesson, you will prove triangles congruent using (1) three pairs of corresponding sides, (2) two pairs of corresponding sides, and one pair of corresponding angles.
This course is based on a textbook that is viewable by clicking on the textbook icon. Keep the textbook open while you go through the lesson so that you may refer to it throughout the lesson.
Additional Resources
Lesson 2: Triangle Congruence by SSS and SAS
Additional Resources(Triangle Congruence by SSS and SAS)
Proceed to the Next Page
Prepare for Practice
Instructions
You have now studied Triangle Statements. It is now time to demonstrate your learning.
Try the activities below on your own. You should be able to answer these before beginning the practice.
Do these activities in your journal.
Activity 1
Given:
Prove:
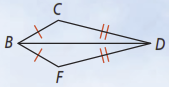
Activity 2
In the figure below, what other information do you need to prove by SAS?
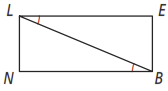
In the figure below, would you use SSS or SAS to prove the triangles are congruent? Explain.
