Unit 4 Lesson 3 Triangle Congruence by ASA and AAS

Unit 4 Lesson 3: Triangle Congruence by ASA and AAS

Introduction to Unit 4 Lesson 3: Triangle Congruence by ASA and AAS

Lesson Overview

ASA vs. AAS

What You Will Learn

understanding the whole meaning of congruence among triangles
- if congruent, then every pair of corresponding parts is also congruent

Additional Resources

Overview

To prove two triangles congruent using the ASA Postulate and the AAS Theorem. You already know that triangles are congruent if two pairs of sides and the included angles are congruent (SAS). You can also prove triangles congruent using other groupings of angles and sides.

Essential Understanding

You can prove that two triangles are congruent without showing that all corresponding parts are congruent. In this lesson, you will prove triangles congruent by using one pair of corresponding sides and two pairs of corresponding angles.

This course is based on a textbook that is viewable by clicking on the textbook icon. Keep the textbook open while you go through the lesson so that you may refer to it throughout the lesson.

Lesson 3: Triangle Congruence by ASA and AAS

Additional Resources (Triangle Congruence by ASA and AAS)

Proceed to the Next Page

Prepare for Application

Instructions

You have now studied Triangle Congruence. It is now time to demonstrate your learning.

Try the activities below on your own. You should be able to answer these before beginning the practice.

Create a journal post called 'Unit 2: Lesson 3 activities' and do these activities in your journal.

Activity 1

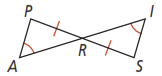
Which two triangles are congruent by ASA? Explain.

Activity 2

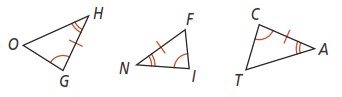
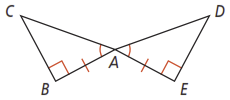
Given: $∠ C A B ≅ ∠ D A E, \bar{B A} ≅ \bar{E A},$ $∠ B$ and $∠ E$ are right angles.

Prove:

Activity 3

Given: $∠ S ≅ ∠ Q$ , $\bar{R P}$ bisects $∠ S R Q$
Prove: $△ S R P ≅ △ Q R P$

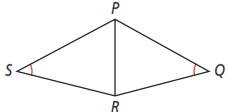
Refer to Problem 3 on page 237 of your textbook. How could you prove $△ W M R ≅ △ R K W$ by ASA? Explain.

Activity 4

In the figure below, are $△ P A R$ and $△ S I R$ congruent? Explain.