Unit 4 Lesson 4 Using Corresponding Parts of Congruent Triangles
Unit 4 Lesson 4: Using Corresponding Parts of Congruent Triangles
Lesson Overview
Corresponding Parts
What You Will Learn
- exploring how triangles that are proven to be congruent will have corresponding part pairs that are also assumed to be congruent
Column 1
With SSS, SAS, ASA, and AAS, you can use three congruent parts of two triangles to show that the triangles are congruent. Once you know that two triangles are congruent, you can make conclusions about their other corresponding parts because, by definition, corresponding parts of congruent triangles are congruent.
Essential Understanding
If you know two triangles are congruent, then you know that every pair of their corresponding parts is also congruent.
This course is based on a textbook that is viewable by clicking on the textbook icon. Keep the textbook open while you go through the lesson so that you may refer to it throughout the lesson.
Additional Resources
Lesson 4: Using Corresponding Parts of Congruent Triangles
Additional Resources (Using Corresponding Parts of Congruent Triangles)
Proceed to the Next Page
Prepare for Application
Instructions
You have now studied the corresponding parts of congruent triangles. It is now time to demonstrate your learning.
Try the activities below on your own. You should be able to answer these before beginning the practice.
Complete the following in your Course Journal
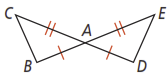
Given: is the midpoint of Prove: |
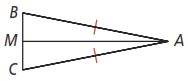
Refer to Problem 2 on page 245 of your textbook. Would the same method work if the landmark were not at sea level? Explain.
Given:
Prove:
