Unit 6 Lesson 1 The Polygon Angle-Sum Theorems
Unit 6 Lesson 1: The Polygon Angle-Sum Theorems
Lesson Overview
Polygons
What You Will Learn
- to find the interior and exterior angles of a polygon
Additional Resources
Overview
In this lesson, you will learn to find the sum of a polygon's exterior and interior angles by a formula. In this textbook, a polygon is convex unless otherwise stated.
- Read Pages 199-205 in your course textbook
Essential Understanding
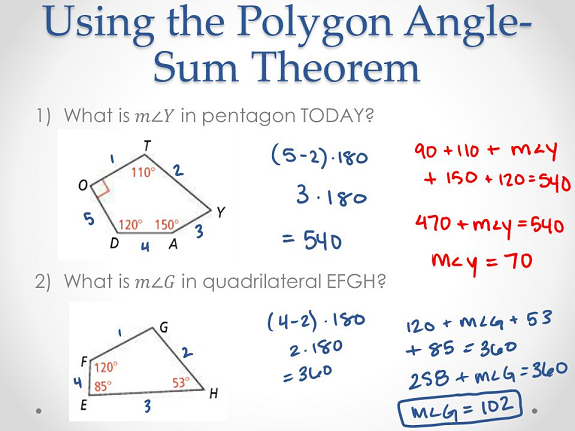
The sum of the interior angle measures of a polygon depends on the number of sides the polygon has. By dividing a polygon with n sides into (n - 2) triangles, you can show that the sum of the interior angle measures of any polygon is a multiple of 180.
Lesson 1: The Polygon Angle-Sum Theorems
Additional Resources (The Polygon Angle-Sum Theorems)
Proceed to the Next Page
Prepare for Application
Instructions
You have now studied Polygon's Angle Sums Theorem. It is now time to demonstrate your learning.
Try the activities below on your own. You should be able to answer these before beginning the practice.
Create an extra journal called 'Unit 6: Lesson 1 activities' and do these in your journal.
- What is the sum of the interior angle measures of a 17-gon?
- The sum of the interior angle measures of a polygon is 1980. How can you find the number of sides in the polygon?
- What is the measure of each interior angle in a regular nonagon?
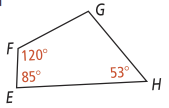
- What is in quadrilateral EFGH shown below?
What is the measure of the exterior angle of a regular nonagon?