Unit 6 Lesson 3 Proving a Quadrilateral is a Parallelogram

Unit 6 Lesson 3: Proving a Quadrilateral is a Parallelogram

Lesson Overview

The Theorems

What You Will Learn

using angle properties to show that lines are parallel
using angle properties to demonstrate that a quadrilateral is a parallelogram

Additional Resources

Overview

In this lesson, you will learn to use angle properties to show that lines are parallel. You will also apply the same properties to show that a quadrilateral is a parallelogram.

Essential Understanding

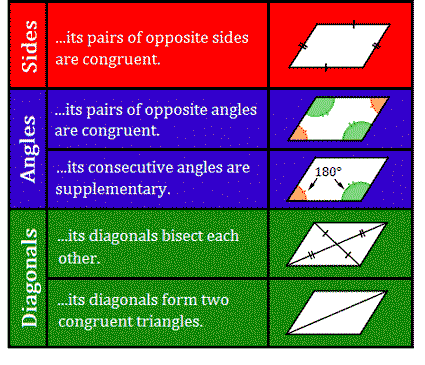
You can decide whether a quadrilateral is a parallelogram if its sides, angles, and diagonals have specific properties. In Lesson 6-2, you learned theorems about the properties of parallelograms. In this lesson, you will learn the converses of those theorems. That is, if a quadrilateral has specific properties, it must be a parallelogram. Theorem 6-8 is the converse of Theorem 6-3.

Read Pages 264-271 in your course textbook.

This course is based on a textbook that is viewable by clicking on the textbook icon. Keep the textbook open while you go through the lesson so that you may refer to it throughout the lesson.

Lesson 3: Proving a Quadrilateral is a Parallelogram

Additional Resources (Proving a Quadrilateral is a Parallelogram)

Proceed to the Next Page

Prepare for Application

Instructions

You have now studied Proving a Quadrilateral is a Parallelogram. It is now time to demonstrate your learning.

Try the activities below on your own. You should be able to answer these before beginning the practice.

Create an extra journal called 'Unit 6: Lesson 3 activities' and do these in your journal.

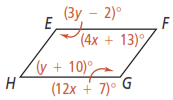
Activity 1

Use the diagram below. For what values of x and y must EFGH be a parallelogram?

Activity 1

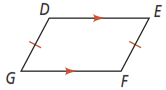
Activity 2

Based on the given information, can you prove that the quadrilateral is a parallelogram? Explain.

Given: $\bar{E F} ≅ \bar{G D}$ , $\bar{D E} ∥ \bar{F G}$
Prove: DEFG is a parallelogram

Activity 2

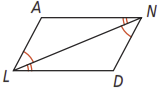
Activity 3

Based on the given information, can you prove that the quadrilateral is a parallelogram? Explain.

Given: $∠ A L N ≅ ∠ D N L$ , $∠ A N L ≅ ∠ D L N$
Prove: LAND is a parallelogram

Activity 4

Refer to Problem 3 on page 371. What is the maximum height that the vehicle lift can elevate the truck? Explain.