Unit 6 Lesson 4 Properties of Rhombuses, Rectangles and Squares
Unit 6 Lesson 4: Properties of Rhombuses, Rectangles and Squares
Lesson Overview
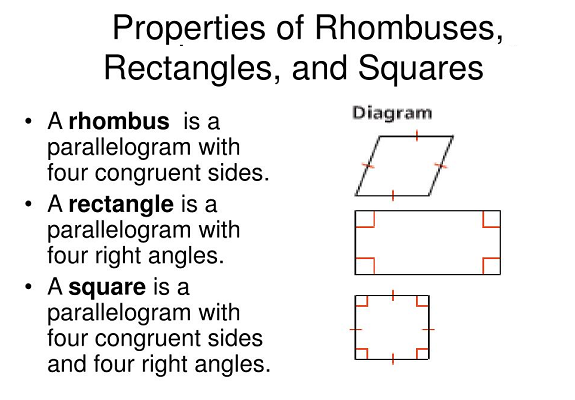
Rhombuses, Rectangles, and Squares
What You Will Learn
- the properties of angles, sides, and diagonals of a trapezoid
Overview
The angles, sides, and diagonals of a trapezoid have specific properties. A trapezoid is a quadrilateral with exactly one pair of parallel sides. The parallel sides of a trapezoid are called bases. The nonparallel sides are called legs. The two angles that share the base of a trapezoid are called base angles. A trapezoid has two pairs of base angles. An isosceles trapezoid is a trapezoid with legs that are congruent.
Read pages 272-285 in your course textbook.
This course is based on a textbook that is viewable by clicking on the textbook icon. Keep the textbook open while you go through the lesson so that you may refer to it throughout the lesson.
Additional Resources
Lesson 4: Properties of Rhombuses, Rectangles and Squares
Additional Resources (Properties of Rhombuses, Rectangles and Squares)
Proceed to the Next Page
Prepare for Application
Instructions
You have now studied the Properties of Rhombuses, Rectangles, and Squares. It is now time to demonstrate your learning.
Try the activities below on your own. You should be able to answer these before beginning the practice.
Create an extra journal called 'Unit 5: Lesson 4 activities' and do these in your journal.
What are the measures of the numbered angles in rhombus PQRS?
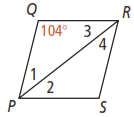
Use the diagram below for questions 1-2.
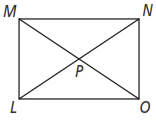
- If LN = 4x - 17 and MO = 2x + 13, what are the lengths of the diagonals of rectangle LMNO?
- What type of triangle is ? Explain.
- A parallelogram has angles of 20, 160, 20, and 160. Can you conclude that it is a rhombus, a rectangle, or a square? Explain.
- Suppose the diagonals of a quadrilateral bisect each other. Can you conclude that it is a rhombus, a rectangle, or a square? Explain.
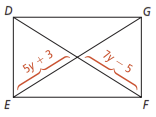
For what value of y is , shown below, a rectangle?
Refer to Problem 3 on page 385. Can you adapt this method slightly to stake off a square play area? Explain.