Unit 6 Lesson 5 Trapezoids and Kites

Unit 6 Lesson 5: Trapezoids and Kites

Lesson Overview

Kites

What You Will Learn

verifying and using properties of special quadrilaterals: trapezoids and kites

Additional Resources

Overview

In this lesson, you will learn to verify and use properties of special quadrilaterals that are not parallelograms: trapezoids and kites.

Read Pages 286-294 in your course textbook

Essential Understanding

A trapezoid is a quadrilateral with exactly one pair of parallel sides. The parallel sides of a trapezoid are called bases. The nonparallel sides are called legs. The two angles that share the base of a trapezoid are called base angles. A trapezoid has two pairs of base angles. An isosceles trapezoid is a trapezoid with legs that are congruent. ABCD at the right is an isosceles trapezoid. The angles of an isosceles trapezoid have some unique properties. Trapezoids also have midsegments. The midsegment of a trapezoid is the segment that joins the midpoints of its legs. The midsegment has two unique properties. A kite is a quadrilateral with two pairs of consecutive sides congruent and no opposite sides congruent. The angles, sides, and diagonals of a kite have specific properties.

This course is based on a textbook that is viewable by clicking on the textbook icon. Keep the textbook open while you go through the lesson so that you may refer to it throughout the lesson.

Lesson 5: Trapezoids and Kites

Additional Resources (Trapezoids and Kites)

Proceed to the Next Page

Prepare for Application

Instructions

You have now studied Trapezoids and Kits. It is now time to demonstrate your learning.

Try the activities below on your own. You should be able to answer these before beginning the practice.

Create an extra journal called 'Unit 6: Lesson 5 activities' and do these in your journal.

Activity 1

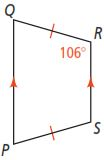In the following diagram, PQRT is an isosceles trapezoid and $m ∠ R = 106$ . What are $m ∠ P$ , $m ∠ Q$ , and $m ∠ S$ ?
Refer to Problem 1 on page 390 of your textbook. If CDEF were not an isosceles trapezoid, would $∠ C$ and $∠ D$ still be supplementary? Explain.

Activity 2

Refer to Problem 2 on page 390 of your textbook. If a fan like this one has 15 angles meeting at the center, what are the measures of the base angles of the trapezoid in the second ring?

Activity 3

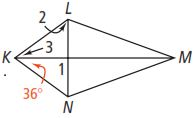
Quadrilateral KLMN shown below is a kite. What are $m ∠ 1$ , $m ∠ 2$ , and $m ∠ 3$ ?

Activity 3

Activity 4

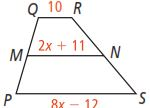
$\bar{M N}$ is the midsegment of PQRS shown below. What is x? What is MN?

How many midsegments can a triangle have? How many midsegments can a trapezoid have? Explain.