Unit 7 Lesson 5 Proportions in Triangles

Unit 7 Lesson 5: Proportions in Triangles

Lesson Overview

Perpendicular Bisectors

What You Will Learn

using proportions to find lengths and segments formed by parallel lines that intersect two or more transversals

Overview

In this lesson, you will learn how to use proportions to find lengths and segments formed by parallel lines intersecting two or more transversals. You will show your learning by using the Side-Splitter Theorem and the Triangle-Angle-Bisector Theorem to find missing parts of triangles.

Essential Understanding

When two or more parallel lines intersect other lines, proportional segments are formed. The bisector of an angle of a triangle divides the opposite side into two segments with lengths proportional to the sides of the triangle that form the angle.

*Source: www.CK-12.org

This course is based on a textbook that is viewable by clicking on the textbook icon. Keep the textbook open while you go through the lesson so that you may refer to it throughout the lesson.

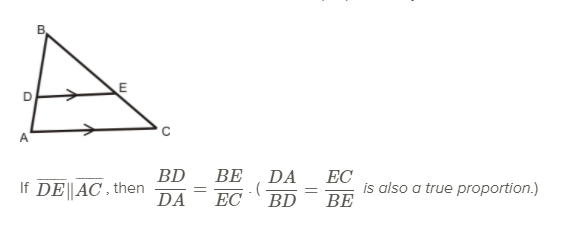
Lesson 5: Proportions in Triangles

Resource Videos

Triangle Proportionality Theorem

Properties of Triangle Proportions

Proceed to the Next Page

Prepare for Application

Instructions

You have now studied Perpendicular and Angle Bisectors. It is now time to demonstrate your learning.

Try the activities below on your own. You should be able to answer these before beginning the practice.

Create an extra journal called 'Unit 7: Lesson 5 activities' and do these in your journal.

Activity 1

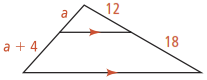
In the diagram below, what is the value of a?

Activity 1

Activity 2

In $△ X Y Z$ , $\bar{R S}$ joins $\bar{X Y}$ and $\bar{Y Z}$ with $R$ on $\bar{X Y}$ and $S$ on $\bar{Y Z}$ , and $\bar{R S} ∥ \bar{X Z}$ . If $\frac{Y R}{R X} = \frac{Y S}{S Z} = 1$ , what must be true about RS? Justify your reasoning.

Activity 3

Refer to Problem 2 on page 347 of your online textbook. What is the length of Site C along the road?

Activity 4

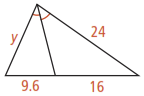
What is the value of y in the diagram below?

Activity 4