Unit 8 Lesson 2 Special Right Triangles
Unit 8 Lesson 2: Special Right Triangles
Lesson Overview
Solving Special Right Triangles
What You Will Learn
- using the proportions in special right triangles to find missing sides
- finding the missing sides in 45-45-90 and 30-60-90 right triangles
Overview
In this lesson, you will learn how to use the proportions in special right triangles to find missing sides. You will show your learning by finding the missing sides in 45-45-90 and 30-60-90 right triangles.
Essential Understanding
Certain right triangles have properties that allow you to use shortcuts to determine side lengths without using the Pythagorean Theorem. The acute angles of a right isosceles triangle are both 45° angles. Another name for an isosceles right triangle is a 45°-45°-90° triangle. Another type of special right triangle is a 30°-60°-90° triangle.
- Read Pages 361-367 in your course textbook by clicking on the textbook icon.
This course is based on a textbook that is viewable by clicking on the textbook icon. Keep the textbook open while you go through the lesson so that you may refer to it throughout the lesson.
Lesson 2 Special Right Triangles
Resource Videos
30-60-90 Triangle
45-45-90 Triangle
Proceed to Next Page
Prepare for Application
Instructions
You have now studied Proving Lines Parallel. It is now time to demonstrate your learning.
Try the activities below on your own. You should be able to answer these before beginning the practice.
Create a journal post called 'Unit 2: Lesson 3 activities' and do these activities in your journal.
Activity 1
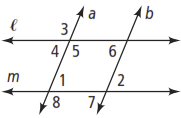
Use the diagram below for the question below:
Which lines are parallel if ? Justify your answer.
Activity 2
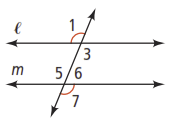
Write a flow proof for the following:
Given:
Prove:
Activity 3
Refer to problem 3 on page 159. What is another way to explain why ? Justify your answer.
Activity 4
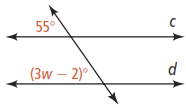
What is the value of w for which in the figure below?
