Unit 10 Lesson 4 Circles and Arcs
Unit 10, Lesson 4: Circles and Arcs
Lesson Overview
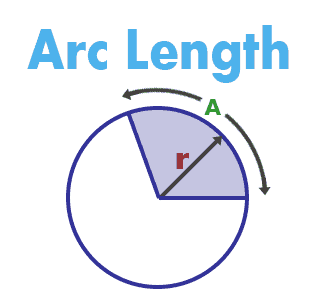
Arcs in Circles
What You Will Learn
- finding the measurements of angles and arcs on a circle
- identifying and finding the circumference and arc length of a circle
Overview
In this lesson, you will learn how to find the measurements of angles and arcs on a circle. You will identify and find the circumference and arc length of a circle.
Essential Understanding
You can find the length of part of a circle's circumference by relating it to an angle in the circle.
- Read pages 428-436 in your course textbook.
Throughout this lesson, you will learn key terms and vocabulary. Write these words down in your journal, and write their definitions as you come across them. They are listed to the right.
This course is based on a textbook that is viewable by clicking on the textbook icon. Keep the textbook open while you go through the lesson so that you may refer to it throughout the lesson.
Lesson 4: Circles and Arcs
Resource Videos
Length of an Arc
Finding Circumference
Proceed to the Next Page
Prepare for Application
Instructions
You have now studied Circles and Arcs. It is now time to demonstrate your learning.
Try the activities below on your own. You should be able to answer these before beginning the practice.
Do these activities in your journal.
Activity 1
Use the figure below for questions 1-3.
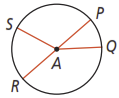
- What are the minor arcs?
- What are the semicircles?
- What are the significant arcs that contain point Q?
Activity 2
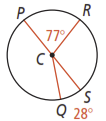
Use the diagram below for questions 1-4. What is the measure of each arc in.
Activity 3
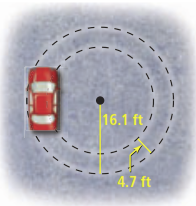A car has a circular turning radius of 16.1 ft. The distance between the two front tires is 4.7 ft. How much farther does a tire on the outside of the turn travel than the tire on the inside?- Suppose the radius of is equal to the diameter of . What is the ratio of the circumference of to the circumference of ?
What is the length of a semicircle with a radius of 1.3 m? Leave your answer in terms of π.