Unit 11 Lesson 1 Space Figures and Cross Sections
Unit 11 Lesson 1: Space Figures and Cross Sections
Lesson Overview
Polyhedrons
What You Will Learn
- using two-dimensional nets to represent a three-dimensional object and to find the shape of cross-sections of three-dimensional figures
- finding vertices, edges, and faces of three-dimensional figures and determining the shape of cross sections of three-dimensional figures

Overview
In this lesson, you will learn to use two-dimensional nets to represent a three-dimensional object and to find the shape of cross-sections of three-dimensional figures. You will show your learning by finding vertices, edges, and faces of three-dimensional figures and determining the shape of cross sections of three-dimensional figures.
Essential Understanding
You can analyze a three-dimensional figure by using the relationships among its vertices, edges, and faces.
- Read Pages 451-458 in your course textbook.
This course is based on a textbook that is viewable by clicking on the textbook icon. Keep the textbook open while you go through the lesson so that you may refer to it throughout the lesson.
Lesson 1: Space Figures and Cross Sections
Proceed to the Next Page
Prepare for Application
Instructions
You have now studied Space Figures and Cross Sections. It is now time to demonstrate your learning.
Try the activities below on your own. You should be able to answer these before beginning the practice.
Do these activities in your journal.
Use the figure below for questions 1-2.
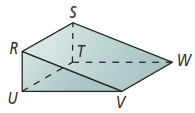
- How many vertices, edges, and faces are in the polyhedron above? List them.
- Is an edge? Explain why or why not.
For each polyhedron, use Euler's Formula to find the missing number.
- faces: __
edges: 30
vertices: 20
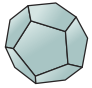
- faces: 20
edges: __
vertices: 12
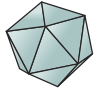
Use the solid below for questions 1-3.
- How can you verify Euler's Formula F + V = E + 2 for the solid?
- Draw a net for the solid.
- How can you verify Euler's Formula F + V = E + 1 for your two-dimensional net?
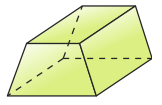
For the solid shown below, what does each of the following planes form the cross-section?
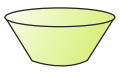
- A horizontal plane
- A vertical plane that divides the solid in half.
Use the figure below for question 1.
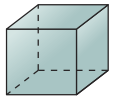
- Draw the cross-section formed by a horizontal plane intersecting the left and right faces of the cube. What shape is the cross-section?



