Unit 11 Lesson 3 Surface Area of Pyramids and Cones
Unit 11 Lesson 3: Surface Area of Pyramids and Cones
Lesson Overview
Biconditionals
What You Will Learn
- naming the faces three-dimensional figures and using formulas to find their areas
- finding the surface area of pyramids and cones

Overview
In this lesson, you will learn to name the faces of three-dimensional figures and use formulas to find their areas. You will show your learning by finding the surface area of pyramids and cones.
Essential Understanding
To find the surface area of a three-dimensional figure, find the sum of the areas of all the surfaces of the figure.
- Read Pages 468-475 in your course textbook.
This course is based on a textbook that is viewable by clicking on the textbook icon. Keep the textbook open while you go through the lesson so that you may refer to it throughout the lesson.
Lesson 3: Surface Area of Pyramids and Cones
Proceed to the Next Page
Prepare for Application
Instructions
You have now studied the Surface Area of Pyramids and Cones. It is now time to demonstrate your learning.
Try the activities below on your own. You should be able to answer these before beginning the practice.
Create a journal post called 'Unit 11: Lesson 3 activities' and do these activities in your journal.
Activity 1
- A square pyramid has base edges of 5 m and a slant height of 3 m. What is the surface area of the pyramid?
- Suppose the slant height of a pyramid is doubled. How does this affect the lateral area of the pyramid? Explain.
Activity 2
- What is the lateral area of the hexagonal pyramid below? Round to the nearest square foot.
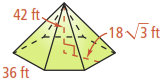
- How does the slant height of a regular pyramid relate to its height? Explain.
Activity 3
The radius of the base of a cone is 16 m. Its slant height is 28 m. What is the surface area in terms of π?
Activity 4
- What is the lateral area of a traffic cone with a radius of 10 inches and a height of 28 inches? Round to the nearest whole number?
- Suppose the radius of a cone is halved, but the slant height remains the same. How does this affect the lateral area of the cone? Explain.



