Unit 3 Lesson 2 Properties of Parallel Lines
Unit 3 Lesson 2: Properties of Parallel Lines
Lesson Overview
Properties of Parallel Lines
Key Terms
- Corresponding Angles Postulate
- Alternate Interior Angles Theorem
- Same-Side Interior Angles Theorem
- Alternate Exterior Angles Theorem
What You Will Learn
- understand the properties of parallel lines and a transversal
- prove theorems about parallel lines
- use properties of parallel lines to find angle measurements
Overview
In this lesson, you will explore the relationships between angles formed by parallel lines and a transversal. You will prove theorems about parallel lines and use properties of parallel lines to find angle measures.
Essential Understanding
The unique angle pairs formed by parallel lines and a transversal are congruent, supplementary, or both.
This course is based on a textbook that is viewable by clicking on the textbook icon. Keep the textbook open while you go through the lesson so that you may refer to it throughout the lesson.
Proceed to the Next Page
Adaptive Practice and Interactives
Explore Parallel and Skew Lines
Parallel or Not?
When two lines are parallel, it means that they do not intersect. Here, you are given a blue line, L, and a second line that passes through point P.
- Move the blue point to make the blue lines parallel.
- The white point represents the intersection of the two lines.
Proceed to the Next Page
Prepare for Application
Instructions
You have now studied Conditional Statements. It is now time to demonstrate your learning.
Try the activities below on your own. You should be able to answer these before beginning the practice.
Do these activities in your journal.
Activity 1
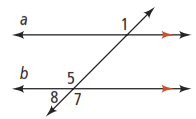
Use the diagram below to find the measure of each angle for questions 1-6. Justify each answer.
- 5
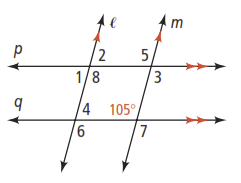
Activity 2
Given:
Prove:
Activity 3
Refer to Problem 1 on page 98 of your textbook. Can you find another way to justify this? Explain.- Using linear pairs, find . Which other angles have that measure? How do you know?
Activity 4
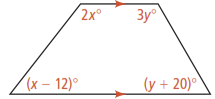Use the following figure for questions 1-2.
- What are the values of x and y?
- What are the measures of the four angles in the figure?