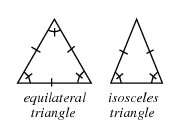
Unit 4 Lesson 5 Isosceles and Equilateral Triangles

Unit 4 Lesson 5: Isosceles and Equilateral Triangles

Lesson Overview

Isosceles Triangle Theorem

Key Terms

Legs of an Isosceles Triangle
The base of an Isosceles Triangle
Vertex Angle of an Isosceles Triangle
Base Angles of an Isosceles Triangle
Corollary
Isosceles Triangle Theorem
Converse of the Isosceles Triangle Theorem
Theorem 4-5
Corollary to Theorem 4-3
Corollary to Theorem 4-4

What You Will Learn

how to classify triangles based only on information about the lengths of their sides
identifying triangles with only information given on the angles

Course Textbook

4.5: Isosceles and Equilateral Triangles, pp 280-291

Overview

In this lesson, you will learn how to classify a triangle based on the lengths of its sides. You will also be able to identify particular triangles based on information about their angles. You will also learn how to use and apply properties of isosceles and equilateral triangles.

Essential Understanding

The angles and sides of isosceles and equilateral triangles have unique relationships. Isosceles triangles are common in the real world. You can frequently see them in structures such as bridges and buildings, as well as in art and design. The congruent sides of an isosceles triangle are its legs. The third side is the base. The two congruent legs form the vertex angle. The other two angles are the base angles.

This course is based on a textbook that is viewable by clicking on the textbook icon. Keep the textbook open while you go through the lesson so that you may refer to it throughout the lesson.

Additional Resources

Applying properties of isosceles triangles

Proceed to the Next Page

Prepare for Application

Instructions

You have now studied isosceles and equilateral triangles. It is now time to demonstrate your learning. Try the activities below on your own.

You should be able to answer these before beginning the practice.

Do these activities in your journal.

Activity 1

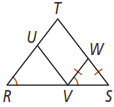Activity 1 Use the figure below for questions 1-2.

1. Is $∠ W V S$ congruent to $∠ S$ ? Is $\bar{T R}$ congruent to $\bar{T S}$ ? Explain.
2. Can you conclude that $△ R U V$ is isosceles? Explain.

Activity 2

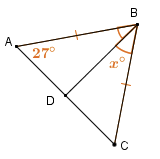
What is the value of x in the figure below?

Activity 2

Activity 3

Refer to Problem 3 on page 253 of your textbook. Suppose the triangles are isosceles triangles, where $∠ A D E$ , $∠ D E C$ , and $∠ E C B$ are vertex angles. If the vertex angles each have a measure of 58°, what are $m ∠ A$ and $m ∠ B C D$ ?